Unit T post #4

Why do sine and cosine NOT have asymptotes, but the four other trig graphs do? 
Well then sine and cosine do not have asymptotes because they will be 1 which will make them 0. There them having no asymptote.  And for the 4 rest trig functions they will have some because even if they are equal to 0 they will have an asymptote Tangent and cotangent at 0 and 180 , or pi. Secant will be 0. As well as cosecant. 

Unit T post #3

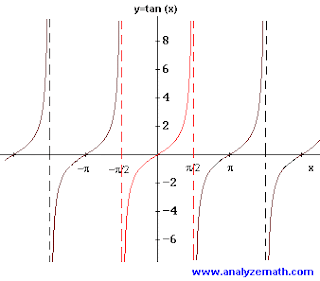
Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill?
This is because there ratios are both over 1. Cotangent is the reciprocal of tangent , there for it will be the exact graph but tangent going from down to up, and cotangent going from top to bottom.

www.analyzemath.com

Unit T post # 2

How do the graphs of sine and cosine relate to each of the others? 

Tangent?  tanx=sinx/cosx. if sine and cosine are positive, tangent is also positive. If one of them is negative, tangent is negative. If both are negative, obviously tangent is positive. Therefore there would be asymptotes where cosx=0, so where x is equal to zero. There would be asymptotes at pi/2 and also at 3pi/2 and it would go on forever. 

Cotangent? cotx=cosx/sinx. The ratio of cosx/sinx because of triangles would be x/y . Therefore, there would be asymptotes where y is equal to 0 which would be at 0 and pi.\

Secant?  Since secant is the reciprocal of cosine, you would have an asymptote where 1/x this will be undefined, so where its x=0 on the unit circle which would be 0 and pi. 

Cosecant? Cosecant is the reciprocal of sine,  1/y. There would be asymptotes where y=0 because i-1/0 is 0. y=0 so there would be asymptotes at pi/2 and 3pi/2 and will go on forever.

Unit T Post #1

How do the trig graphs relate to the Unit Circle? 
A. Period ? Why is the period for sine and cosine 2pi, where as the period for tangent and cotangent is pi? 
The period for sine and cosine is 2pi because the period infers to how long it takes to repeat the patterns of positive and negative values based on the different quadrants. Also, for sine how we know its 2pi because the pattern is positive to positive to negative to negative, which is one full rotation . and is similar to cosine.  On the other hand for tangent and cotangent it takes half of the unit circle to repeat the pattern of positives or negatives so there period is pi. 
B. Amplitude? How does the fact that sine and cosine have amplitudes of one ( and the trig functions don't have amplitudes) relate to what we know about the Unit Circle? 
This most importantly is related in how the radius of the circle is 1. The greatest values that are on the unit circle to the left and the right is 1 as well as up and down. picture: www.rasmus.is

Assessment #4

http://www.youtube.com/watch?v=jO3x00GzlKo&feature=youtu.be

Assessment #3

http://www.youtube.com/watch?v=fNUjHNVbvOg&feature=youtu.be

Assessment #2

Well the sum formula and the half angle formula , are one of the same. They are both correct ways to solve a problem. The answers dont seem to be the same but if we plug them into our calculator they will be the same. I made a mistake on the sum formula I ment to put + rad3 on the Tan. So it is the same    just a different way to do it.  Its the same because for one you use exact unit circle measures by splitting it into two , and for the half angle you are doubling it to get something alike but that is just one angle.